Elektrizitätslehre

E 5.2 Lecherleitung - ausführliche Versuchsbeschreibungen

→ Kurzbeschreibung von Versuchen

Demonstrationsversuche mit Dezimeterwellen

1. Einführung - etwas Physik

1.1 Die Lecherleitung

Die Lecherleitung besteht aus zwei parallelen Drähten, deren Abstand groß gegen den Drahtdurchmesser ist. Auf den Anfang der Lecherleitung wird eine hochfrequente Wechselspannung mit

          (Gl. 1)

gegeben, die sich längs der Lecherleitung mit der Geschwindigkeit v  fortpflanzt, so dass an der Stelle x  zwischen den Drähten die Spannung

          (Gl.2)

herrscht.

1.2 Verhältnisse an der kurzgeschlossenen Lecherleitung

Wird das Ende der Lecherleitung kurzgeschlossen, so ist dort der Strom maximal, und wegen des Kurzschlusses ist die Spannung null. Ferner entsteht am kurzgeschlossenen Ende eine reflektierte Spannungswelle, die gegenüber der hinlaufenden Welle eine Phasenverschiebung π besitzt und für die gilt:

          (Gl.3)

Die reflektierte Welle interferiert mit der einfallenden Welle, sodass sich stehende Wellen ergeben mit:

          (Gl.4)

wobei x  der von der kurzgeschlossenen Stelle aus gemessene Abstand ist. Dies bedeutet, dass an den Stellen, die k • λ/2 von dem Kurzschluss entfernt sind, die Spannung ihr Minimum erreicht. Es bildet sich also an diesen Stellen ein Spannungsknoten aus. Ferner ist die stehende Spannungswelle mit einer ebenfalls stehenden Stromwelle verbunden. Da die hinlaufende Stromwelle bei der Reflexion keinen Phasensprung erleidet, gilt für die stehende Stromwelle:

          (Gl.5)

wobei x  der von der kurzgeschlossenen Stelle, die (2k - 1) • λ/4 von dem Kurzschluss entfernt sind, der Strom sein Minimum erreicht. Es bildet sich also an diesen Stellen ein Stromknoten aus.

1.3 Verhältnisse am der offenen Lecherleitung

Wird das Ende der Lecherleitung offen gelassen, so ist dort die Spannung maximal und wegen des offenen Endes der Strom null. Ferner entsteht am offenen Ende eine reflektierte Stromwelle, die gegenüber der hinlaufenden Welle eine Phasenverschiebung π besitzt und für die gilt:

          (Gl.6)

Die reflektierte Welle interferiert mit der einfallenden Welle, so dass sich stehende Wellen ergeben mit:

          (Gl.7)

wobei x  der von der offenen Stelle aus gemessene Abstand ist.

Dies bedeutet, dass an den Stellen, die k • λ/2 von dem offenen Ende entfernt sind, der Strom sein Minimum erreicht. Es bildet sich also an diesen Stellen ein Stromknoten aus. Ferner ist die stehende Stromwelle mit einer ebenfalls stehenden Spannungswelle verbunden. Da die hinlaufende Spannungswelle bei der Reflexion keinen Phasensprung erleidet, gilt für die stehende Spannungswelle:

          (Gl.8)

wobei x  der von der offenen Stelle aus gemessene Abstand ist.

Dies bedeutet, dass an den Stellen, die (2k - 1) • λ/4 von dem offenen Ende entfernt sind, die Spannung ihr Minimum erreicht. Es bildet sich also an diesen Stellen ein Spannungsknoten aus.

1.4 Verhältnisse an der mit dem Wellenwiderstand abgeschlossenen Lecherleitung

Schließt man das Ende der Lecherleitung mit einem Widerstand ab, dessen Wert so gewählt ist, dass weder die Stromwelle noch die Spannungswelle reflektiert werden, so treten naturgemäß entlang der Lecherleitung keine Strom- und Spannungsbäuche bzw. Knoten auf. Die gesamte am Anfang eingespeiste Energie wird verlustlos übertragen und von dem Widerstand aufgenommen. Der erforderliche Widerstandswert für den reflexionsfreien Abschluss ist gleich dem sogenannten Wellenwiderstand Z der Lecherleitung. Er lässt sich aus den geometrischen Daten der jeweiligen Lecherleitung errechnen.

          (Gl.9)

     d = Abstand zwischen den Drähten, r = Drahtradius

Der Wellenwiderstand einer verlustlosen Paralleldrahtleitung ist demnach nur von der Querschnittsgestaltung und nicht von der Frequenz abhängig. Der Wellenwiderstand für verschiedene Paralleldrahtleitungen liegt meist im Bereich zwischen 100 Ω und 800 Ω. Für eine Lecherleitung wie sie in den folgenden Versuchen verwendet wird mit: d = 2 cm und r = 0,2 cm ist:

Z = 120 Ω ln (2 cm / 0,2 cm) = 276 Ω

Dieser Wert entspricht ungefähr dem in der Praxis gebräuchlichen Wert von 300 Ω für Bandleitung wie sie in einfachen Antennenanlagen verwendet wird.

1.5 Nachweis von Strombäuchen und Spannungsbäuchen

Die Spannungsbäuche d. h. die Stellen entlang einer Lecherleitung wo die Spannung maximal ist können mit einer sogenannten Feldindikatorlampe nachgewiesen werden. Diese besteht aus einer Glimmlampe, an die eine feste Spannung angelegt wird, die knapp unterhalb der Zündspannung liegt. Eine geringe zusätzliche äußere Spannung in der Nähe, z. B. von einem Spannungsbauch stammend, bewirkt eine Überschreitung der Zündspannung und somit ein helles Aufleuchten, der meist schon schwach glimmenden Glimmlampe.

Der Nachweis der Spannungsbäuche kann aber auch dadurch erfolgen, dass man einen Tastkopf, bestehend aus einem λ/4 langen Stück Lecherleitung dessen Ende mit einer Glühlampe abgeschlossen ist, mit seinem offenen Ende direkt über der Lecherleitung parallel entlang führt. Bei den Spannungsbäuchen findet dann eine Energieübertragung statt, so dass die Glühlampe aufleuchtet.

Die Strombäuche d. h. die Stellen entlang einer Lecherleitung wo der Strom maximal ist können mit einem Tastkopf, bestehend aus einem λ/2 langen Stück Lecherleitung, dessen Ende mit einer Glühlampe abgeschlossen ist und das mit seinem geschlossenen Ende direkt über der Lecherleitung parallel entlang geführt wird, nachgewiesen werden. In den Strombäuchen findet dann eine Energieübertragung von der Lecherleitung auf das abgestimmte System des Tastkopfes statt, so dass die Glühlampe aufleuchtet.

1.6 Verhältnisse am Dipol

Klappt man ein Stück Paralleldrahtleitung mit offenem Ende um 90° auf, so entsteht ein sogenannter Hertzscher Dipol. An den Enden des Hertzschen Dipols, dessen Länge die Hälfte der speisenden Wellenlänge beträgt, ist die Spannung maximal und der Strom null. In der Mitte wo eingespeist wird ist der Strom maximal und die Spannung null.

1.7 Die Dipolantenne Bei einer Paralleldrahtleitung verläuft das elektromagnetische Feld senkrecht von Leiter zu Leiter als homogenes transversales Feld. Nähert man sich dem Leitungsende so spreizen sich die Feldlinien immer mehr auf, werden kreisbogenförmig und dringen nach außen in den freien Raum. Das so von dem Dipol abgestrahlte Wellenfeld breitet sich in alle Richtungen senkrecht zur Achse des Dipols aus. In Achsrichtung selbst erfolgt keine Abstrahlung. Um einer maximale Abstrahlung zu erreichen, muss der Wellenwiderstand der speisenden Leitung frei sein. Der Strahlungswiderstand Z eines Dipols errechnet sich nach:           (G l.10) Wobei der Durchmesser des Dipols klein gegenüber seiner Länge ist. l = Länge des Dipols, λ = Wellenlänge Der Wellenwiderstand eines λ/2 Dipols ist also für l = 69 cm: 80 • π2 • (34,5 cm/69,0 cm)2 = 197 Ω

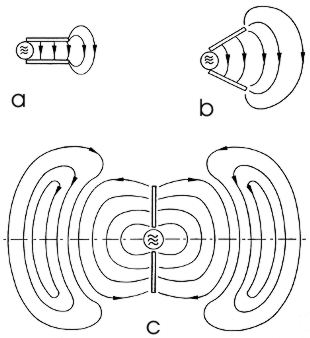Abb. 1: Ablösung elektromagnetischer Wellen am Dipol

In der Praxis wählt man die Dipollänge um 10 % kürzer als λ/2, d. h. in diesem Fall ist der λ/2 Dipol 31 cm lang, so wie er auch in den Versuchen verwendet wird. Der Grund dafür ist der, dass sich elektromagnetische Wellen entlang von Leitungen, wegen der unvermeidlichen Leitungskapazitäten und Induktivitäten, langsamer ausbreiten als im freien Raum und zwar um den Faktor 0,7 bis 0,8. Wegen des Zusammenhanges

          (Gl.11)

muss deshalb bei konstanter Frequenz n die Wellenlänge geringer sein, wenn sich die Ausbreitungsgeschwindigkeit verringert.

1.8 Dielektrizitätskonstante

Zwischen den beiden Leitern eines Paralleldrahtsystems besteht eine Kapazität, deren Größe vom Leiterabstand und von dem Medium zwischen den Leitern abhängt. Durch Einfügen eines dielektrischen Stoffes zwischen den Leitern wird die Kapazität im Vergleich zu Luft bei gleichem Leiterabstand erhöht.

Dielektrische Stoffe sind elektrisch nichtleitend, also Isolatoren, und durchlässig für elektrische Felder.

Dielektrische Stoffe sind z. B. Wasser, Luft, Glas, Gummi, Stickstoff, Petroleum, Äthylalkohol.

Meist wird die Dielektrizitätskonstante e von Luft gleich 1 gesetzt und die der anderen Stoffe darauf bezogen. Je nach dem Wert der Dielektrizitätskonstante, des zwischen den Leitern eingebrachten Stoffes, verringert sich die Ausbreitungsgeschwindigkeit im Vergleich zu Luft. Dies kann man zeigen, indem man die Wellenlänge λ-Luft und dann für λ-Flüssigkeit mit dem Glühlampen-Tastkopf bestimmt. Zur Messung von λ-Flüssigkeiten wird die Lecherleitung in einem Trog mit der jeweiligen Flüssigkeit geführt.

Wegen G1.11 gilt dann:

          (Gl.12) und
          (Gl.13)     c = Lichtgeschwindigkeit in Luft bzw. in Vakuum

Setzt man Gl. 12 ins Verhältnis zu Gl. 13 ergibt sich:

          (Gl.14)

und somit:

          (Gl.15)

Da für die Geschwindigkeit allgemein gilt:

          (Gl.16)

folgt bei Einsetzten von Gl. 16 in Gl. 15:

          (Gl.17)

Dies bedeutet, dass bei e = 1 für Luft, das e des untersuchten Stoffes sich direkt aus dem Verhältnisquadrat der gemessenen Wellenlängen ergibt.

In dem Versuch zur Bestimmung der Dielektrizitätskonstante von Wasser wird aus versuchspraktischen Gründen anders vorgegangen. In diesem Versuch wird gezeigt, dass ein λ/2 Dipol in Luft länger ist als ein solcher in Wasser, um die eingestrahlte Leistung aufzunehmen und eine Glühlampe zum Leuchten zu bringen.

1.9 Amplitudenmodulation und Demodulation Bei der Amplitudenmodulation (Abb. 2) wird die Amplitude einer hochfrequenten Trägerschwingung durch die niederfrequente Schwingung eines Tonfrequenzsignales geändert. Entscheidend beim Vorgang der Amplitudenmodulation ist die Tatsache, dass die niederfrequente Signalschwingung nicht zur hochfrequenten Trägerschwingung addiert, sondern die Amplitude der Trägerschwingung im Rhythmus der niederfrequenten Signalschwingung moduliert wird. Genauer ausgedrückt: Es wird bei der Amplitudenmodulation zur Amplitude U0 der hochfrequenten Trägerschwingung        der Momentanwert der niederfrequenten Schwingung      addiert, sodass sich eine modulierte Schwingung      ergibt.

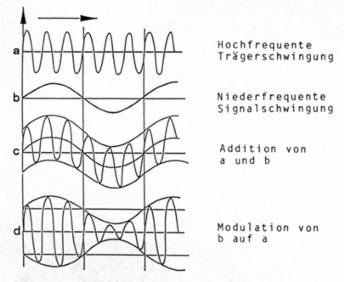Abb. 2: Amplitudenmodulation

Die Frequenz der Trägerschwingung bleibt unverändert, das niederfrequente Signal ist in der Einhüllenden enthalten.

Abb. 3: Prinzipschaltung zur Modulation, drahtlosen Übertragung und Demodulation

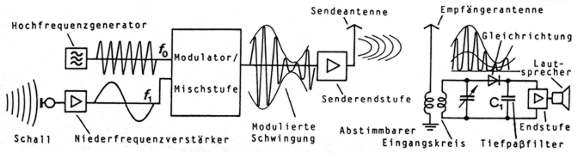
Bei der Demodulation eines amplitudenmodulierten Trägers gilt es, die Hüllkurve von der Trägerschwingung zu trennen. Durch Gleichrichtung wird eine Halbschwingung des empfangenen und durch einen Schwingkreis vorselektierten, modulierten Trägers unterdrückt. Man erhält somit eine pulsierende Gleichspannung, die aus einem niederfrequeten Wechselspannungsanteil und einem hochfrequenten Wechselspannungsanteil besteht. Durch Filterung z. B. mit einem RC-Tiefpassfilter, wird der hochfrequente Anteil unterdrückt und der niederfrequente Anteil, der das ursprüngliche Signal darstellt, bleibt übrig. Dieser wird dann verstärkt und in einem Lautsprecher hörbar gemacht.

1.1. Versuchsziel

Darstellung der Strom- und Spannungsmaxima und -minima an einer Lecherleitung mit offenem Ende und geschlossenem Ende. Messung der Wellenlänge.

1.2. Bauteile und Geräte 1 Dezimeterwellensender 1 Lechersystem mit Zubehör 1 Feldindikatorlampe 1 Stabilisierendes Netzgerät 0 bis 300 V 1 Rollbandmaß 1.3 Aufbau (Abb. 6)

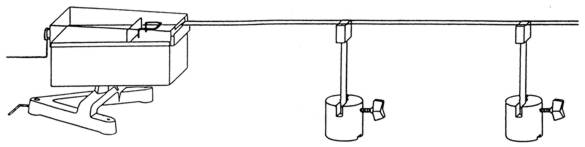Abb. 6: Aufbau von Dezimeterwellensender und Lecherleitung

1.4. Durchführung

a) Nachweis der Spannungsmaxima-Bestimmung der Wellenlänge

Dezimeterwellensender und Lecherleitung ist wie in Abschnitt 3 beschrieben und wie in Abb. 6 aufgebaut. Feldindikatorlampe an das Netz anschließen und an einem der beiden Leiter vom offenen Ende beginnend langsam entlangfahren. Dabei die Stelle entlang der Lecherleitung markieren, an der die Feldindikatorlampe zum erstenmal aufleuchtet. Kontinuierlich weiterfahren und die Stelle markieren, an der sie verlischt. In der Mitte zwischen den Markierungen liegt das Spannungsmaximum. Abstand zwischen dem (offenen) Leitungsende und ermittelten Spannungsmaximum mit dem Rollbandmaß messen. Der sich ergebende Wert ist λ/2.

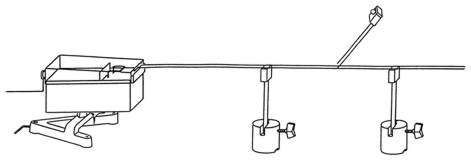Abb. 7: Nachweis von Spannungsmaxima mit den Glühlampentastkopf

Man kann auch die Spannungsmaxima nachweisen, in dem man wie in Abb. 7 dargestellt, den Tastkopf mit Glühlampe mit seinem offenen Ende knapp über der Lecherleitung entlangführt, (unter einem Winkel von 45° gegenüber der horizontalen), ohne die Lecherleitung zu berühren. Den Tastkopf dabei nur am Plastikgehäuse anfassen und möglichst weit von sich weghalten. Keinesfalls die Zuführung zum Tastkopf oder die Lecherleitung selbst berühren. Die Glühlampe leuchtet im Bereich der Spannungsmaxima auf.

b) Nachweis der Strommaxima

Zum Nachweis der Strommaxima wird auf den Tastkopf mit Glühlampe ein l/4 Kurzbügel aufgesteckt. Dieser wird dann mit seinem geschlossenen Ende knapp über der Lecherleitung entlang geführt, (unter einem Winkel von 45° gegenüber der horizontalen) ohne die Lecherleitung zu berühren. Die Glühlampe leuchtet im Bereich der Strommaxima auf.

c) Nachweis der Strom- und Spannungsmaxima an der offenen Lecherleitung

Weisen Sie entlang der Lecherleitung mit offenem Ende alle Spannungsmaxima und Strommaxima nach und zeichnen Sie eine maßstäbliche Skizze.

d) Nachweis der Strom- und Spannungsmaxima an der kurzgeschlossenen Lecherleitung

Weisen Sie entlang der Lecherleitung mit geschlossenem Ende alle Spannungsmaxima und Strommaxima nach und zeichnen Sie eine maßstäbliche Skizze.

1.5. Ergebnisse

zu 1.4 a)
Der Abstand des ersten Spannungsmaximums vom offenen Leitungsende beträgt 34,5 cm entsprechend λ/2. Demnach beträgt die Wellenlänge λ = 69 cm.

zu 1.4 c)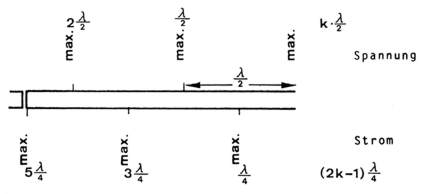 Abb. 8a: Strom- und Spannungsverteilung bei der offenen Lecherleitung

zu 1.4 d)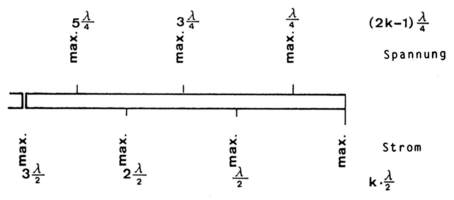 Abb. 8b: Strom- und Spannungsverteilung bei der kurzgeschlossenen Lecherleitung

2.1. Versuchsziel

Darstellung der Strom- und Spannungsmaxima und -minima auf einer Lecherleitung mit Schleifendipol am Ende und am Dipol selbst.

2.2. Bauteile und Geräte 1 Dezimeterwellensender 1 Lechersystem mit Zubehör 1 Feldindikatorlampe 1 Stabilisierendes Netzgerät 0 bis 300 V 2.3 Aufbau (Abb. 9)

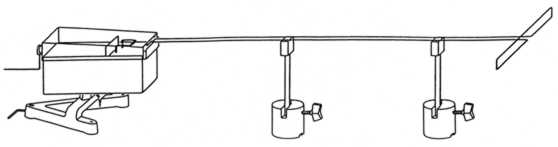Abb. 9: Lecherleitung mit aufgestecktem Schleifendipol

2.4. Durchführung

a) Nachweis der Spannungsmaxima

Weisen Sie mit der Feldindikatorlampe die Stellen entlang des Lechersystems und am Dipol nach, wo sich die Spannungsmaxima befinden. Dabei das Lechersystem möglichst stark an den Dezimeterwellensender ankoppeln. Dies erreicht man im allgemeinen dadurch, dass man die Schleife der Lecherleitung mit der Schleife im Dezimeterwellensender zur Überlappung bringt.

b) Nachweis der Strommaxima

Weisen Sie mit dem Tastkopf mit Glühlampe und aufgestecktem l/4 Kurzschlussbügel die Stellen entlang der Lecherleitung und am Dipol nach, so sich die Strommaxima befinden.

2.5. Ergebnisse

zu 2.4 a)
Entlang der Lecherleitung sind keine Spannungsmaxima nachweisbar. Nur an den beiden Dipolenden findet man jeweils ein Spannungsmaximum.

zu 2.4 b)
Entlang der Lecherleitung sind keine oder nur sehr schwache Strommaximum nachweisbar.

3.1. Versuchsziel - Bestimmung der Abstrahlrichtung eines Sendedipols. - Feststellung der Polarisationsrichtung. - Messung der Empfangsfeldstärke durch einen Empfangsdipol mit Gleichrichtung und Anzeigeinstrument. - Untersuchung der Wirkung eines Reflektorstabes. 3.2. Bauteile und Geräte 1 Dezimeterwellensender 1 Stabilisierendes Netzgerät 0 bis 300 V 1 Wechselskalenmessinstrument, Grundgerät 1 Aktives Messmodul 3 V / 10V 1 kleiner Stativfuß, V-förmig 1 Sockel 2 Experimentierkabel, 2 m, rot 3.3 Aufbau (Abb. 10)

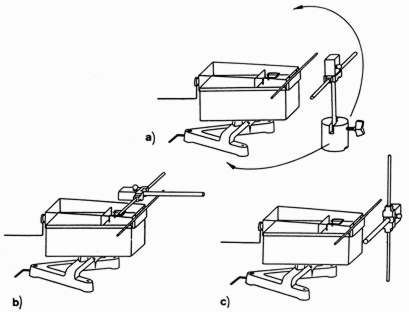Abb. 10: Nachweis der Abstrahlrichtung und Polarisation einer Dipolantenne

3.4.Durchführung

a) Bestimmung der Abstrahlrichtung eines Sendedipols

1. Entsprechend Abb. 10a Dezimeterwellensender mit vorn eingespannten Dipol in Betrieb nehmen und Empfangsdipol mit Glühlampe ca. 20 cm parallel zum Sendedipol ausgerichtet aufstellen, so dass das Glühlämpchen leuchtet. Dann den Empfangsdipol im Halbkreis um den Sendedipol bewegen.

2. Entsprechend Abb. 10b Empfangsdipol mit Glühbirnchen wieder wie zu Beginn parallel zur Achse des Sendedipols ausrichten, so dass das Glühlämpchen leuchtet. Dann den Empfangsdipol unter Behaltung der Parallelität langsam im Halbkreis schwenkend in eine Position über den Sendedipol bringen.

Ergebnisse notieren.

b) Feststellen der Polarisationsrichtung

Entsprechend Fig. 10c Dezimeterwellensender mit vorn eingespanntem Dipol in Betrieb nehmen und Empfangsdipol mit Glühlampe ca. 20 cm parallel zum Sendedipol ausgerichtet aufstellen, so dass das Glühlämpchen leuchtet. Dann den Empfangsdipol senkrecht zu Tischfläche ausrichten.

Ergebnisse notieren.

c) Bestimmung der Feldstärke durch einen Empfangsdipol mit Gleichrichter und Anzeigeinstrument sowie Untersuchung der Wirkung eines Reflektorstabes Aufbau gemäß Abb. 11 vornehmen. Dabei insbesondere beachten dass: -   das Messinstrument sich möglichst weit außerhalb des direkten Strahlungsfeldes des Senders befindet d. h. das Messinstrument am besten seitlich vom Sendedipol aufstellen. -   der Abstand zwischen Sendedipol und Empfangsdipol so eingestellt wird, dass sich bei einem Messbereich von 3 V~ ein Zeigerauschlag von ca. 2/3 des Vollausschlages erreicht wird.

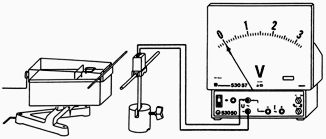Abb. 11: Bestimmung der Feldstärke mit einem Messinstrument

Dann einen Dipolstab mittig anfassend und möglichst weit von sich weg haltend parallel zum Sendedipol von hinten annähern und den Zeigerausschlag am Messinstrument beobachten. Gegebenenfalls den Reflektordipol an einem Plastiklineal befestigen.

Ergebnisse notieren.

3.5. Ergebnisse

zu 3.4 a)
1. Seitlich vom Sendedipol verlöscht das Glühlämpchen am Empfangsdipol. Dies bedeutet, dass die größte Feldstärke vor dem Sendedipol entsteht, in Achsrichtung wird fast gar nichts abgestrahlt.
2. Das Glühlämpchen am Empfangsdipol bleibt an. Dies bedeutet, dass die Feldstärke in allen Richtungen parallel zur Achse des Sendedipols hoch ist.

zu 3.4 b)
Das Glühlämpchen am Empfangsdipol verlöscht. Dies bedeutet, dass das vom Dipol abgestrahlte Wellenfeld horizontal polarisiert ist.

zu 3.4 c)
In bestimmten Abständen des Reflektordipols vom Sendedipol wird das nach vorne abgestrahlte elektromagnetische Feld verstärkt oder geschwächt. Ähnliches kann man mit vor dem Sendedipol angebrachten Dipolen, sogenannte Direktoren erreichen. Bei Antennen werden häufig mehrere Direktoren und Reflektoren so angebracht, dass eine Feldverstärkung nach vorne auftritt, unter gleichzeitiger Schwächung der seitlichen und nach hinten gerichteten Abstrahlung.

4.1. Versuchsziel - Darstellung der Wellenverkürzung durch Wasser im Vergleich zu Luft. - Ableitung der Dielektrizitätskonstante von Wasser basierend auf dem Wellenlängevergleich. 4.2. Bauteile und Geräte 1 Dezimeterwellensender 1 Stabilisierendes Netzgerät 0 bis 300 V 1 Satz Dipole im Wassertank 1 kleiner Stativfuß, V-förmig 1 Spritzflasche, 2 Liter 4.3 Aufbau (Abb. 13)

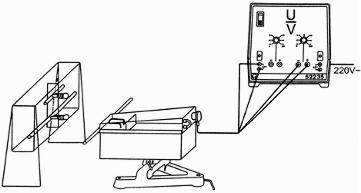Abb. 13: Untersuchung der Dielektrizitätskonstante von Wasser

4.4. Durchführung

Als erste je ein 3,8 V Glühlämpchen in die Lampenfassungen am Wassertank einschrauben. Der Satz Dipole im Wassertank wird so vor den laufenden Dezimeterwellenwender gestellt, dass das Glühlämpchen des unteren Dipols aufleuchtet. Dann langsam Wasser einfüllen. Sobald der untere Dipol mit Wasser bedeckt ist, erlischt das zugehörige Glühlämpchen. Wird der obere Dipol vom Wasser vollständig bedeckt, so leuchtet das entsprechende Glühlämpchen schwach auf. Damit ist gezeigt, dass die Wellenlänge bei gleicher Sendefrequenz im Wasser wesentlich geringer ist als in Luft. Mit diesem Ergebnis lässt sich auf die unterschiedliche Ausbreitungsgeschwindigkeit elektromagnetischer Wellen in verschiedenen Medien sowie auf die starke Zunahme der Dielektrizitätskonstante ε in Wasser schließen.

Hinweis:
Das Längenverhältnis der beiden Dipole ist nicht wie eigentlich zu erwarten 1:9 (ε-Wasser: 81) sondern etwa 1: 5.5 entsprechend einem ε von ca. 30. Dies liegt im wesentlichen daran, dass die Dielektrizitätkonstante von Wasser im Dezimeterwellengereich wesentlich von 81 abweicht. Hinzu kommen noch Störungen der Dipolresonanz durch die an den Dipolen angebrachten Glühlampen, die eine effektive Dipolverlängerung speziell beim kurzen Dipol bewirken.