 |
Schwingungen und Wellen |
3.3 Interferenz
| Aufgabe
Demonstration des ungestörten Durchdringens zweier Kreiswellen und der vektoriellen Addition ihrer Elongationen. Das bei der Interferenz zweier Kreiswellen entstehende Wellenbild besteht aus einem System konfokaler Hyperbeln, deren räumliche Lage zeitlich konstant ist. In einem Punkt P tritt Auslöschung ein, wenn gilt (Abb. 1):   E1, E2 : Erregerzentrum 1, Erregerzentrum 2 Verstärkung tritt ein, wenn 
Die geometrischen Orte all dieser Punkte sind konfokale Hyperbeln mit den Brennpunkten in den Erregerzentren. Auf den Hyperbeln der Verstärkung verlaufen fortschreitende Wellen. Die Richtung der Interferenzhyperbeln wird durch den Winkel zwischen der geradlinigen Verlängerung dieser Hyperbeln und dem Lot auf  gekennzeichnet. Die geradlinigen Verlängerungen gehen annähernd durch die Mitte von  (Abb. 2). Genau genommen gilt dies nur für die Asymptoten der Hyperbeln. Die Minima erscheinen unter den Winkeln
 (1) |
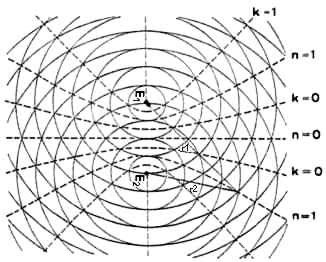 Abb. 1: Interferenz zweier Kreiswellen mit dem Abstand der Wellenzentren n : Hyperbeln der Verstärkung, k : Hyperbeln destruktiver Interferenz 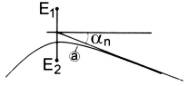 Abb. 2: Zur Definition der Richtungen αn, unter denen die Interferenzminima erscheinen; a n-te Interferenzhyperbel für Interferenzminimum |
Geräte
1 Wellenwanne mit
2 Doppelerreger (28) (29)
3 Blenden aus Acrylglas (37)
1 Blendenhalter (38)
1 Erreger für ebene Wellen (30)
3 Blattfolien
1 Lineal
1 Winkelmesser
1 AV-Farbstift
zusätzlich: Klebeband
3.3.1 Interferenz zweier durch Doppelerreger erzeugter Kreiswellen
| Aufbau Einen der Erreger in Halter (5) schieben. Schraube (5.2) so weit lockern, bis beide Erregerspitzen auf dem Wannenboden aufliegen. Durch Anziehen von Schraube (5.1) Erreger in Halter befestigen und mit Schraube (5.2) so weit anheben, daß beide Erregerspitzen gerade in die Wasseroberfläche eintauchen. Erreger und Stroboskop einschalten und Amplitude über Amplitudensteiler so einstellen, daß beide Kreiswellensysteme scharf werden. Erforderlichenfalls Eintauchtiefe über Schraube (5.2) nachstellen. Stroboskop abschalten. Folie auf Beobachtungsschirm befestigen. Durchführung Mit Amplitudensteiler kurze Wellenzüge erzeugen und die ungestörte Durchdringung der beiden Wellenzüge beobachten. Dann Interferenzfeld ausgedehnter Wellenzüge bei eingeschaltetem, danach bei abgeschaltetem Stroboskop und bei verschiedenen Frequenzen betrachten. Für eine bestimmte Frequenz f Lage der Interferenzhyperbeln und der Erregerzentren auf der OHP-Folie einzeichnen (alternativ hierzu: fotografisch auswerten). Für quantitative Auswertungen die zugehörige Wellenlänge λ und den Erregerabstand d im Messprotokoll aufnehmen. Versuch mit zweitem Doppelerreger wiederholen. Für quantitative Auswertungen wie zuvor Interferenzhyperbeln und Erregernzentren auf zweiter Folie einzeichnen und zugehörige Wellenlänge und Erregerabstand im Meßprotokoll aufnehmen. Auswertung und Ergebnis Die von den Erregern ausgehenden Kreiswellen durchdringen sich ungestört. Bei der Interferenz zweier Kreiswellen liegen die Punkte mit maximaler Amplitude oder mit Amplitude Null (als graue Streifen erkennbar) auf konfokalen Hyperbeln mit den Erregerzentren als Brennpunkten. |
Messbeispiel Abb. 3: Inerferenz zweier Kreiswellen; Erregerabstand d = 5,5 cm
 Abb. 4: Erreger 2 - λ = 1,1 cm; d = 8 cm |
Die Beziehung (1) wird qualitativ bestätigt, wenn bei zunehmender Frequenz die Öffnung der Interferenzhyperbeln weiter wird. Entsprechend wird die Öffnung der Hyperbeln weiter bei Austausch des Erregers mit d = 5,5 cm gegen den Erreger mit d = 8 cm bei gleicher Frequenz (Abb. 3/Abb. 4). Außerdem nimmt mit zunehmender Öffnung (d.h. abnehmender Wellenlänge) die Zahl der Hyperbeln zu.
Hinweis
Zur Zahl der Hyperbeln: Da sin α ≤ 1 folgt aus (1)
Zur quantitativen Bestätigung von (1) ermittelt man die Winkel αn zwischen den geradlinigen Verlängerungen der Interferenzhyperbeln wie in Abb. 3/4 und der Symmetrieachse.
Die Winkel αn können direkt gemessen werden und mit den nach Beziehung (1) berechneten (mit den gemessenen Werten für λ und d) Werten für αn verglichen werden (siehe Tabelle).
3.3.2 Interferenz zweier von engen Spalten ausgehender Kreiswellen (Beugung am Doppelspalt)
Aufgabe
Beobachtung des Interferenzfeldes hinter einem Doppelspalt.
| Aufbau Erreger für ebene Wellen (30) einsetzen. Aus Blenden (37) und Blendenhalter einen Doppelspalt zusammenstecken. Spaltbreite ca. 5 mm. Der Spaltmittenabstand ist dann d = 55 mm. Aufbau nach Abb. 5: Doppelspalt. Die abgeflachten Seiten des Spaltes dem Erreger zuwenden. Welle mit λ ≈ 1 cm erzeugen (Abbildungsmaßstab beachten!), Amplitude auf einen so großen Wert stellen, daß das Interferenzfeld hinter dem Doppelspalt deutlich sichtbar wird. Stroboskop anschalten; Folie am Beobachtungsschirm befestigen. Durchführung Frequenz variieren und dabei die Veränderung der Beugungsminima beobachten. Für quantitative Auswertungen für eine Frequenz (z.B. 20 Hz) die Lage der Interferenzhyperbeln und die Lage des Spaltes auf die Folie zeichnen. Die Größen d und λ im Meßprotokoll festhalten. Zuletzt bei eingeschaltetem Stroboskop beobachten. |
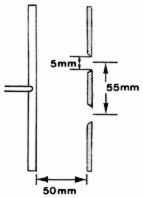 Abb. 5: Doppelspalt |
Messbeispiel Abb. 6: Interferenzfeld hinter einem Doppelspalt
αn : Richtung der Beugungsminima λ = 1,0cm; d = 5,5 cm (fotografische Auswertung) |
Auswertung und Ergebnis
Jeder Spalt wird zum Ausgangspunkt einer neuen Kreiswelle (vgl. Huygenssches Prinzip Abschnitt 3.4). Das entstehende Wellenbild gleicht also dem, das durch die Doppelerreger erzeugt wird. Die Öffnung und die Zahl der Interferenzhyperbeln wird mit zunehmender Wellenlänge kleiner. Die Beziehung (1) ist auch hier anwendbar. Zur quantitativen Bestätigung der Anwendbarkeit von Beziehung (1) ermittelt man die Winkel αn zwischen den geradlinigen Verlängerungen der Interferenzhyperbeln wie in Abb. 6 und der Symmetrieachse und vergleicht αn mit den nach Beziehung (1) ermittelten Winkeln αntheor (siehe Messbeispiel). |