Schwingungen und Wellen

SW 2.6 Wellenwanne mit stroboskopischer Beleuchtung - Versuchsbeschreibungen

Aufgaben

Untersuchung des Einflusses von Hindernissen und Spalten verschiedener Abmessungen d auf die Ausbreitung ebener Wellen (d: Spaltbreite bzw. Breite des Hindernisses):

a) d » λ
b) d ≈ λ
c) d « λ

Quantitative Bestätigung der Beziehung

          (1)

für die Lage der Beugungsminima beim Spalt.

Geräte

Wellenwanne mit

1 Erreger für ebene Wellen (39)
3 Blenden aus Acrvlglas (37)
1 Blendehalter (38)
2 Blenden aus Acrylglas (36)
Spülmittel
1 Blatt Folie
1 Lineal
1 Winkelmesser
1 AV-Farbstift, mittelfein
zusätzlich: Klebeband
1 Schraube z.B. Ø = 0,5 cm

Bei allen Versuchen Erregeramplitude am Amplitudensteiler so einstellen, daß das Wellenbild hinter dem Hindernis bzw. Spalt scharf wird.

Zum Einstellen bestimmter Wellenlängen Stroboskop einschalten. Die abgeflachten Seiten der Blenden werden immer dem Erreger zugewandt. Bei stroboskopischer Betrachtung erforderlichenfalls Erregeramplitude vergrößern. Für alle Wellenlängenangaben ist zu beachten, daß



ist (λ = Wellenlänge auf dem Beobachtungsschirm).

Aufbau Erreger für ebene Wellen einsetzen und Wellen mit einer Frequenz von ca. 15 Hz anregen. Eine der großen Blenden aus (37) parallel zum Erreger im Abstand von ≤ 5 cm aufstellen und als beugende Halbebene benutzen. Zunächst ohne, dann bei eingeschaltetem Stroboskop betrachten. Durchführung Erregerfrequenz variieren. Erforderlichenfalls Erregeramplitude anpassen. Bei stroboskopischer Betrachtung evtl. Erregeramplitude vergrößern. Wellenfeld im "Schatten" der Halbebene beobachten.

Messbeispiel Abb. 1: Beugung an einer Halbebene, f ca. 15 Hz Auswertung zu Versuch 3.4.1 am Ende, im Anschluß an Abschnitt 3.4.3 "Die Ausbreitung hinter Spalten".

3.4.2 Ausbreitung hinter Hindernissen Aufbau Zunächst eine ebene Welle der Wellenlänge von ca. λ = 1,2 cm erregen. Im Abstand von ca. 5 cm großes Hindernis parallel zum Erreger in die Wellenwanne stellen (z.B. eine der Blenden (36), Beugungslöcher über der Wasseroberfläche). Durchführung a) d » λ; breites Hindernis - Beugung an einer Halbebene. Erregerfrequenz variieren. Erforderlichenfalls Erregeramplitude anpassen. Bei stroboskopischer Betrachtung Erregeramplitude vergrößern. Wie in den folgenden Fällen die Abhängigkeit des Wellenbildes im "Schatten" des Hindernisses von der Wellenlänge beobachten. Zunächst ohne, dann bei eingeschaltetem Stroboskop beobachten. 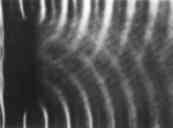Abb. 2: Ausbreitung hinter einem breiten Hindernis d = 9 cm   λ = 2 cm b) d ≈ λ Breites Hindernis durch ein Hindernis von etwa der Größe der Wellenlänge ersetzen (z.B. eine der Blenden aus (37) aufrecht gestellt). Zunächst bei Wellenlängen in der Größenordnung von ca. 1 cm beobachten, dann Wellenlänge variieren. Mit und ohne Stroboskop beobachten. Abb. 4: Ausbreitung hinter einem Hindernis von der Größe der Wellenlänge d = 2,5 cm   λ = 1,2 cm c) d « λ Hindernis aus b) durch ein im Vergleich zur Wellenlänge kleines Hindernis ersetzen (z.B. auf dem Kopf stehende Schraube, die aus dem Wasser herausragt) und im Abstand von ca. 15 cm vom Erreger aufstellen. Mit dem Amplitudensteller kurze Wellenzüge erzeugen und die vom Beugungszentrum ausgehende Welle beobachten. Bei ausgedehnten Wellenzügen ohne Stroboskop beobachten (Die vom Hindernis ausgehende Welle ist auf der dem Erreger zugewandten Seite gut zu erkennen). 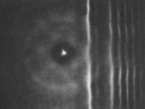Abb. 6: Ausbreitung nach Auftreffen auf ein im Vergleich zur Wellenlänge kleines Hindernis; ebener Wellenzug hat Hindernis bereits passiert; Messbeispeile zur Ausbreitung hinter Hindernissen vgl. Abb. 2/4/6. Die Auswertung der Versuche 3.4.2 a) - c) im Anschluss an Abschnitt 3.4.3 "Die Ausbreitung hinter Spalten".

3.4.3 Ausbreitung hinter Spalten Aufbau Aus den beiden großen Blenden aus (37) mit dem Blendenhalter einen im Vergleich zur Wellenlänge λ breiten Spalt herstellen (d = 6 cm). Spalt parallel zum Erreger im Abstand von 5 cm aufstellen und mit dem Wellenerreger ebene Wellen erzeugen. Durchführung a) d » λ. Erregerfrequenz variieren und mit und ohne Stroboskop beobachten. Erforderlichenfalls Erregeramplitude anpassen. Wie in den folgenden Fällen die Abhängigkeit des Wellenbildes im "Schatten" des Spaltes von der Wellenlänge beobachten. Abb. 3: Ausbreitung hinter einem breiten Spalt b) d ≈ λ - Beugung am Spalt: Folie am Beobachtungsschirm befestigen: Spalt auf etwa die Größe der Wellenlänge verkleinern, aber λ ≤ d. Spalt aus Blenden aus (36) in Blendenhalter und in geringem Abstand vom Erreger aufstellen (z.B. dSpalt = 2 cm). • Die Beobachtung ohne Stroboskop liefert für kleine Frequenzen deutlichere Ergebnisse. Bei seitlicher Betrachtung werden die Beugungsrninima deutlicher. Wellenlänge λ von kleinen Werten ausgehend stufenweise vergrößern und Veränderungen des Wellenbildes hinter dem Spalt beobachten. • Empfehlenswerte Daten für λ und d : λ = 0,7 cm; d = 2 cm (vgl. Fig. 5). Andere Kombinationen von λ und d sind möglich, z.B. λ = 1 cm, d = 2 cm oder λ = 0,5 cm, d = 1 cm, eingeschaltetes Stroboskop. Die Richtung α des ersten Beugungsminimums auf der Folie markieren und die Spaltbreite und die zugehörige Wellenlänge messen. Wellenlänge in kleinen Schritten erhöhen bzw. verkleinern, bis die Abhängigkeit der Richtung der Beugungsminima von der Wellenlänge erkennbar wird. • Die Beugungsminima sind nur schwach ausgeprägt. Sollte die Richtung des ersten Minimums nicht erkannt werden, nach Beziehung (1) für die gewählte Kombination von λ und d α1 berechnen und auf der Folie einzeichnen. Wellenfeld in diesem Winkelbereich untersuchen. Abb. 5: Ausbreitung hinter einem Spalt von der größe der Wellenlänge, d = 2 cm, λ = 0,7 cm, α1 = 22,5°, α1 = Richtung des ersten Beugungsminimums; Beugung am Spalt; c) d « λ Spaltbreite dSpalt auf die Größe einer Wellenlänge oder weniger verkleinern (λ  ≥dSpalt, z.B. dSpalt = 0,7 cm). Engen Spalt nahe an Erreger aufstellen. Erregeramplitude groß wählen. Wellenlänge λ von großen Werten ausgehend stufenweise verkleinern und die Veränderung des Wellenbildes hinter dem engen Spalt beobachten. Abb. 7: Ausbreitung hinter engen Spalten, d < 1 cm; d = 0,7 cm, λ = 1,2 cm Hinweis Empfehlenswerte Daten für λ und d vgl. Abb. 7. Mit und ohne Stroboskop betrachten. Erforderlichenfalls auch mit engeren Spalten arbeiten und erneut Wellenlänge variieren.

Auswertungen und Ergebnisse

Ausbreitung hinter Halbebenen:
Die Wellen breiten sich nicht nur in dem von der Halbebene freigelassenen Teil aus, sondern greifen im Bogen auch in den "Schatten" hinein. Sie dringen dort wie kreisförmige Wellen mit der Kante der Halbebene als Zentrum ein. Im Schattenraum sind sie wesentlich schwächer als im Gebiet der geradlinigen Ausbreitung. Lange Wellen zeigen das Verhalten deutlicher als kurze.

Ausbreitung hinter Hindernissen:
Die beiden Begrenzungen des im Vergleich zur Wellenlänge großen Hindernisses wirken wie Halbebenen. In den Schattenraum greifen kreisförmige, schwächere Wellen über. Das breite Hindernis zeigt schon im Abstand weniger Wellenlängen verwaschene Grenzen (Abb. 2).
Sind Hindernis und Wellenlänge etwa gleich groß (d ≈ λ), entsteht im Schattenraum eine deutliche Struktur. Die Lage der entstehenden Beugungsminima und -maxima hängt von der Wellenlänge ab (Abb. 4).

Ist das Hindernis im Vergleich zur Wellenlänge klein (d « λ), so geht eine neue kreisförmige, aber schwache Welle vom Hindernis aus (Abb. 6).

Ausbreitung hinter Spalten:
Die beiden Kanten eines breiten Spaltes (d » λ) wirken wie die Kanten einer Halbebene: In die Schattenräume greifen kreisförmige, schwächere Wellen über (Abb. 3).

Ist die Spaltbreite etwa gleich der Wellenlänge (d ≈ λ), treten im Schattenraum Richtungen ohne Wellenbewegung (Minima) auf. Unter größeren Winkeln ist wieder eine schwächere Wellenbewegung sichtbar (Abb. 5). Das erste Beugungsminimum erscheint für zunehmende Wellenlängen (d.h. für zunehmendes Verhältnis λ/d) unter größeren Winkeln.

Beziehung (1) ergibt für k = 1 die Richtung des ersten Beugungsminimums:

α_1theor.mit

λ = 0,7 cm, d = 2 cm, k = 1

_1theor. = 20,5°

Der im Experiment gefundene Wert α_1exp. = 22,5° stimmt gut mit diesem Wert überein.

Spalte von der Breite einer Wellenlänge oder weniger erzeugen keine Beugungsminima mehr. Die Wellen breiten sich hinter dem Spalt so aus, als befände sich im Spalt ein punktförmiger Wellenerreger (Abb. 7).

Das bedeutet:

Jeder Punkt einer Wellenfläche kann als Ausgangspunkt einer neuen Kreiswelle (Elementarwelle) betrachtet werden (Huygenssches Prinzip 1).

Die bei den Versuchen auftretende Abweichung von der geradlinigen Ausbreitung (Beugung) ist wellenlängenabhängig und hängt vom Verhältnis der Spalt- bzw. Hindernisgröße zur Wellenlänge ab (Je kleiner die Verhältnisse sind, um so stärker werden die Wellen gebeugt).