Schwingungen und Wellen

SW 2.6 Wellenwanne mit stroboskopischer Beleuchtung - Versuchsbeschreibungen

3.7 Brechung ebener Wellen an ebenen Grenzflächen

Aufgabe

Untersuchung des Verhaltens von Wellen an einer ebenen Grenzfläche zwischen Gebieten mit unterschiedlichen Wassertiefen, die Medien unterschiedlicher Dichte darstellen. Überprüfung des Brechungsgesetzes.

Die Wellenlänge und damit die Phasengeschwindigkeit von Wasserwellen hängt bei gegebener Frequenz von der Wassertiefe ab (vgl. 3.6). Dem "dichteren Medium" entsprechen Gebiete kleinerer Wassertiefe; dem "dünneren Medium" größere Wassertiefen. Gebiete verschiedener Wassertiefe werden durch Einlegen von (Acryl)Glasplatten in die Wellenwanne geschaffen.

Trifft eine ebene Welle unter einem Winkel α ≠ 90° auf die Trennfläche zwischen tiefem und flachem Wasser, dann wird sie in Fortpflanzungsrichtung und Wellenlänge geändert. Es gilt das Brechungsgesetz:

(1)

α = Einfallswinkel
β = Brechungswinkel
v₁,λ₁ = Geschwindigkeit bzw. Wellenlänge in Medium 1
v₂,λ₂ = Geschwindigkeit bzw. Wellenlänge in Medium 2
n_1,2 = Brechzahl für das betreffende Medienpaar
f = Erregerfrequenz

Geräte

Wellenwanne mit

1 Erreger für ebene Wellen (30)
1 Planparallele Platte (33)
1 Glasdreieck
2 Blattfolien
1 Farbstift
1 Winkelmesser
1 Lineal
Spülmittel

3.7.1 Übergang vom "dünneren" ins "dichtere" Medium Aufbau

Planparallele Platte nahe am ebenen Erreger in die Wellenwanne legen. Wasserstand zunächst niedriger als die Dicke der Platte wählen. Vorsichtig Wasser bei laufendem Erreger (niedrigste Frequenz) zugießen, bis die Brechung deutlich sichtbar wird. Erforderlichenfalls Erregeramplitude vergrößern.

Hinweis

Optimaler Wasserstand über der Platte ca. 2 - 3 mm. Bei zu niedrigem Wasserstand zu große Dämpfung, bei zu hohem Wasserstand Brechzahl n zu klein.

Folie am Beobachtungsschirm befestigen.

Durchführung

Stroboskop einschalten und auf der Folie Richtung der einfallenden Welle, der gebrochenen Welle und der Mediengrenze einzeichnen. Wellenlänge vor und über der planparallelen Platte messen.

Erregerfrequenz stufenweise erhöhen und dabei die Richtung der einmal gebrochenen Welle in Abhängigkeit von der Erregerfrequenz beobachten.

Bei nierigster Erregerfreuenz die Richtung der einfallenden Welle durch Verändern der Postition des Wellenerregers verändern und wie zuvor die Richtung der einfallenden und der einmal gebrochenen Welle auf der Folie einzeichnen.

Wellenlänge im "dünneren" und in "dichteren" Medium messen.

Ber der Erregerfrequenz von ca. 10 Hz Erregeramplitude erhöhen bis auch hinter der Platte ein Wellenfeld sichtbar wird. Richtung der zweinmal gebrochenen Welle mit der Richtung der vom Erreger erzeugten Welle vergleichen. Mit und ohne Stroboskop beobachten.

Messbeispiel

Abb. 1: Berechnung an einer planparallelen Platte

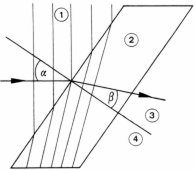Abb. 2: Auswertungsbeispiel einer Folie

Tabelle 1

α	β	sinα/sinβ	λ₁/cm	λ₂/cm	λ₁/λ₂
38°	24°	1,51	2,0	1,3	1,54
46°	35°	1,25	2,1	1,5	1,4

α = 38° = Einfallswinkel
β = 24° = Brechungswinkel
λ₁ = 2,0 cm
λ₂ = 1,3 cm

(1) und (3) = dünneres Medium
(2) = dichteres Medium
(4) = Einfallslot

Auswertung und Ergebnisse

Die ebene Welle wird beim Übergang vom dünneren ins dichtere Medium zum Lot hin gebrochen. Das Brechungsgesetz kann qualitativ und - mit den Ergebnissen nach Tabelle 1 - quantitativ bestätigt werden.

Steigert man die Frequenz, so wird die Welle an der Mediengrenze (1)-(2) (Abb. 2) weniger stark gebrochen, die Brechzahl wird kleiner.

Erklärung

Der Unterschied der Wellenlängen in Gebieten verschiedener Wassertiefe und damit der Unterschied der Ausbreitungsgeschwindigkeiten wird mit zunehmender Frequenz geringer (vgl. Versuch 3.6/Abb. 4). Dabei ist die Abnahme der Steigung der Funktion λ = f(h) bei verschiedenen Wassertiefen stärker als aufgrund der Zunahme der Frequenz zu erwarten ist. (Die Geschwindigkeitsdifferenz des "Medienpaares" bei niedrigen Frequenzen unterscheidet sich von der bei höheren Frequenzen; Dispersion).

Das bedeutet, dass die Geschwindigkeit c (bzw. die Wellenlänge λ) neben der Wassertiefe noch durch andere Faktoren beeinflußt wird.

Der Zusammenhang zwischen c, λ und ν (bei h = const.) wird im Versuch Dispersion untersucht. Dort wird sich zeigen, daß die Phasengeschwindigkeit c von der Wellenlänge abhängt, und damit kann die Frequenzabhängigkeit der Brechzahl eingeordnet werden.

Die Brechzahl ist frequenzabhängig. Hohe Frequenzen werden weniger stark gebrochen.

Aus Abb. 4 - Versuch 3.6 kann auch entnommen werden, warum die Wassertiefe h über der planparallelen Platte nur wenige mm betragen soll. Für Wassertiefen von einigen mm ist die Steigung der Kurven λ als Funktion von h (h : Wassertiefe) besonders groß, also die Änderung der Wellenlänge beim Übergang auf die Planparallele Platte besonders groß.

Die Wellenfronten der doppelt gebrochenen Welle Gebiet (3) Abb. 2 sind parallel zu denen der primären Welle. Auch beim Übergang vom dichteren ins dünnere Medium findet Brechung statt. Die Welle wird dabei vom Lot weggebrochen (Übergang (2) nach (3)) und zwar um dem gleichen Winkel, um den die Welle beim Übergang ins dichtere Medium (Übergang (1) nach (2)) zum Lot hingebrochen wird.

3.7.2 Übergang vom "dichteren ins dünnere" Medium

Aufbau

Die planparallele Glasplatte durch die dreieckige Glasplatte ersetzen. Den ebenen Wellenerreger parallel zu einer Kathete ausrichten, so daß die Hypothenuse brechende Kante zwischen "dichtem und dünnem" Medium wird. Wasserstand über der Glasplatte ca. 2 - 3 mm. Ebene Welle mit ca. 35 Hz bei abgestelltem Stroboskop anregen. Erregeramplitude so wählen, daß die ins dünnere Medium einlaufende Welle deutlich sichtbar wird.

Folie am Beobachtungsschirm befestigen.

Durchführung

Frequenz der Wellenerregung stufenweise erniedrigen. Dabei die Richtung der ins "dünnere Medium" gebrochenen Welle und der an der "Mediengrenze" reflektierten Welle beobachten. Mit und ohne Stroboskop beobachten. Erforderlichenfalls Erregeramplitude anpassen.

Für quantitative Aussagen bei der niedrigsten Frequenz auf der Folie zeichnen.

Messbeispiel

α = 52°   Einfallswinkel
β = 68°   Brechungswinkel
λ₁ = 1,9 cm   Wellenlänge über der Glasplatte
λ₂ = 2,3 cm   Wellenlänge im tiefen Wasser
α' = 52°

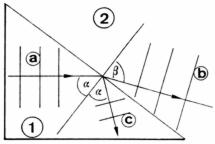Abb. 3a: Berechnung beim Übergang ins dünnere Medium
(1)  dichtes Medium
(2)  dünnes Medium
(a)  einfallende Welle
(b)  gebrochene Welle
(c) an der Mediengrenze reflektierte Welle

Abb. 3b: fotografische Auswertung;
Beobachtung der gebrochenen Welle

Abb. 3b: fotografische Auswertung;
Beobachtung der an der Mediengrenze reflektierten Welle

Auswertung und Ergebnis

Die ebene Welle wird beim Übergang ins dünnere Medium vom Lot weggebrochen.

Der Brechungswinkel wird für abnehmende Frequenzen gröber (vgl. auch Auswertung 3.7.1). Die Brechung erfolgt auch hier nach dem Brechungsgesetz:

Aus dem Messbeispiel 2 folgt:

Der Strahlengang bei der Brechung ist also umkehrbar.

Die Wellen werden zum Teil an der Mediengrenze in das flache Wasser (das dichtere Medium) zurückreflektiert (Reflexionswinkel = Einfallswinkel).

Für abnehmende Frequenzen wächst der Brechungswinkel und der Anteil der in das flache Wasser zurückreflektierten Welle (der Anteil der Reflexion hängt auch vom Unterschied der Brechungsindizes ab, d.h. vom Unterschied der Wassertiefen).

An der Grenzfläche zwischen 2 Gebieten mit verschiedenen Brechungsindizes erfolgt also eine teilweise Reflexion.

Wäre eine weitere Frequenzerniedrigung möglich, dann würden die Wellen bei einer bestimmten Frequenz um 90° vom Lot weggebrochen.