Mechanik

 -R     -S    

M 7.3   Reflexion zweier oder mehrerer Bälle am Boden (Superjump)

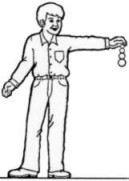
1. Handhabung Stecken Sie einen der kleinen Bälle oben auf die Stange und lassen Sie die ganze Ball-Pyramide mit dem großen Ball unten aus etwa einem halben Meter Höhe so nach unten fallen, dass die ganze Anordnung möglichst senkrecht auf den harten Boden aufprallt. Halten Sie die Ball-Pyramide mit ausgestrecktem Arm weit von sich weg. Der kleine Ball springt mehrere Meter hoch. Falls die Ball-Pyramide nicht senkrecht aufkommt, springt der Ball schräg weg. Aber keine Angst: Zwei Ersatzbälle sind vorhanden.

2. Etwas Physik

Mit Hilfe von Impuls- und Energiesatz lässt sich die Springballaufgabe behandeln. Ein gewisser Rechenaufwand lässt sich dabei nicht umgehen. Zunächst sei das für nur zwei Bälle gezeigt.

Betrachten wir zuerst den Fallvorgang in aufeinanderfolgenden Phasen: Beide Bälle werden aus der Höhe h₀ gemeinsam fallengelassen. Sie haben dabei keinen direkten Kontakt miteinander. Achten Sie darauf, dass die Höhe h₀ in jedem Fall größer ist als der Durchmesser der beiden Bälle. Am Boden haben beide eine Geschwindigkeit v₀, die sich aus der Höhe errechnen lässt. Für den Ball 1 mit der Masse m₁, gilt dann:

0,5m₁(v₀)² = m₁gh₀.   Daraus folgt: v₀ = √(2gh₀)

Die vom Boden zurückspringenden Bälle sind nicht ideal, d.h.: Lässt man einen Ball aus der Höhe h0 herunterfallen, kommt er unten mit der Geschwindigkeit v0 an und springt mit verminderter Geschwindigkeit v0' nur bis zur Höhe h0' wieder hoch, da beim Verformen der elastischen Bälle etwas Energie verlorengeht. Man definiert eine sogenannte Stoßzahl ε - auch Stoßziffer k oder Restitutionskoeffizient genannt -, die durch das Verhältnis der Relativgeschwindigkeiten vor und nach dem Stoß gegeben ist, d. h. ε = v0'/ v0. Aus dem Energiesatz ergibt sich auch für v0' = √(2gh0'). Damit kann man schreiben ε = v0'/v0 = √(h0'/h0) Die Stoßzahl ε lässt sich also einfach durch Messen der Ausgangs- und der Rücksprunghöhe bestimmen. Für die hier betrachteten Bälle gilt etwa ε ≈ 0,9.

In der zweiten Phase wird der Ball 1 vom Boden mit der Geschwindigkeit v1a reflektiert und bewegt sich dann wieder aufwärts. In diesem Fall gilt v1a = ε · v0, wobei das Suffix a hier für Anfang, das Suffix e für Ende stehen soll. Ball 2 fällt kurz hinter Ball 1 mit der Geschwindigkeit v2a nach unten; für ihn gilt v2a = - v0 (das negative Vorzeichen ist notwendig, da sich der Ball entgegengesetzt zum Ball 1 bewegt).

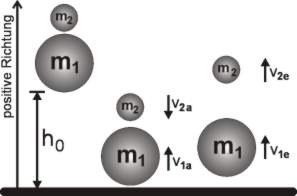In der nächsten Phase ist Ball 2 von Ball 1 abgeprallt und springt mit der Geschwindigkeit v_2e nach oben. Ball 1 springt auch noch nach oben, jedoch mit der veränderten Geschwindigkeit v_1e. Der Impulssatz lautet dann allgemein,
m₁ · v_1a + m₂ · v_2a = m₁ · v_1e + m₂ · v_2e

Mit der verallgemeinerten Definition für

ergibt sich aus dem Impulsatz:

Formel (1)

Setzt man die Werte: v_1a = ε · v₀ und v_2a = - v₀

Formel (1a)

Diese Formel lässt einige Forderungen zu. Je kleiner m₂ ist, um so größer wird die Rückprallgeschwindigkeit v_2e, d.h. um so höher springt auch der Ball 2. Im idealen Fall mit m₂ = 0 und ε = 1 ergibt sich v_2e = 3 · v₀. Auf die Höhe umgerechnet ergibt sich aus h₂ / h₀ = (v_2e / v₀)² : h₂ = 9 · h₀, d.h. das Neunfache der Ausgangshöhe.

Im realen Fall mit m₁ = 52 g (größter Ball) und m₂ = 4,5 g (kleinster Ball) und ε = 0,9 ergibt sich v_2e = 2,3 · v₀, d.h. für die erreichbare Höhe immerhin noch h₂ = 5,3 h₀.

Das Experiment ist real auch durchführbar, wenn man vorsichtig die Plastikstange aus dem größten Ball herauszieht. Setzt man in das Loch des untersten Balles ein Streichholz oder einen dünnen Metallstift ein, lassen sich beide Bälle miteinander verbinden, und man kann sie gleichzeitig fallenlassen. Mit etwas Glück erreicht man mit dieser nicht sehr gut optimierten Anordnung das Vier- bis Fünffache der Ausgangshöhe.

Betrachtet man nun eine Anordnung mit drei übereinander befindlichen Bällen, kann man mit den getroffenen Vereinbarungen weiterrechnen: m₁ wird zu m₂, m₂ → m₃, v_1a → v_2a, v_2a → v_3a. Der Wert von ε bleibe der Einfachheit halber konstant. Man könnte ihn auch noch unterscheiden mit ε₁₂ bzw. ε₂₃ usw. Damit ergibt sich aus Formel (1)

Formel (2)

Setzt man für v_2e den in Formel (1a) errechneten Wert und für v_3a = - v₀ ein, ergibt sich mit den Bezeichnungen q₁ = m₂ / m₁ und q₂ = m₃ / m₂ nach einigen Umformungen

Formel (2a)

Das ist nun keine sehr handliche Formel mehr. Relativ leicht sieht noch der Idealfall aus: m₃ « m₂, d. h. q₂ ≈ 0 und m₂ « m₁, d.h. q₁ ≈ 0 sowie e = 1. Damit ergibt sich v_3e = 7 v₀ bzw. für die erreichbare Sprunghöhe h₃ = 49 · h₀, d.h. das Neunundvierzigfache der Ausgangshöhe.

Setzt man reale Werte ein mit m₁ = 52 g (größter Ball), m₂ = 8g (der kleinere der mittleren Bälle) und m₃ = 4,5g (kleinster Ball) sowie ε = 0,9, ergibt sich v_3e ≈ 2,8 · v₀ bzw. für die erreichbare Sprunghöhe h₃ ≈ 7,9 · h₀. Nimmt man für m₂ = 24g (der größere der mittleren Bälle), ergibt sich v_3e ≈ 3 · v₀ bzw. für die erreichbare Sprunghöhe h₃ ≈ 9 · h₀. Diese Experimente kann man mit etwas Geschick auch selbst durchführen.

Als letztes soll schließlich der Fall mit allen vier Bällen behandelt werden. Entsprechend der Notation wird m₂ → m₃, m₃→m₄, v_2e→v_3e, v_3a→v_4a.Damit folgt

Formel (3)

Setzt man hier den Wert von v_3e aus Formel (2a) ein und nimmt für v_4a = -v₀, ergibt sich mit den Bezeichnungen q₁ = m₂ / m₁, q₂ = m₃ / m₂ und q₃ = m₄ / m₃

Formel (3a)

Setzt man die Massen der Bälle (m₁ = 52g, m₂ = 24g, m₃ = 8g, m₄ = 4,5g) sowie ε = 0,9 ein, ergibt sich v_4e ≈ 5,7 · v₀ bzw. für die erreichbare Sprunghöhe h₄ ≈ 32 · h₀.

Ließe man die Anordnung mit vier Bällen aus 1 m Höhe auf einen harten Boden fallen, resultierte daraus eine Sprunghöhe von 32m für den kleinsten Ball. Natürlich wird das in Wirklichkeit nicht erreicht, weil diverse Faktoren (Reibung, schräges Abprallen) dieses Ergebnis verhindern. Im idealen Fall ergäbe sich sogar h₄ = 225 · h₀.

Es lassen sich noch eine Reihe weiterer Betrachtungen anstellen, die an dieser Stelle nur angedeutet werden sollen. Ein eher scherzhaftes Beispiel:
Wie viel Bälle wären im idealen Fall nötig, um den obersten Ball ins Weltall zu schießen? Die Antwort lautet: Beim Fall aus 1 m Höhe würden dazu schon 12 Bälle ausreichen. Im Idealfall würde bei n Bällen eine Endgeschwindigkeit von v_n =(2ⁿ - 1) · v₀ erreicht. Die Anfangsgeschwindigkeit v₀ beträgt beim Fall aus 1m Höhe v₀ = √2gh = 4,43 m/s. Setzt man die Fluchtgeschwindigkeit mit v_n = 11,3 km/s an, ergibt sich aus der Auflösung der Gleichung 11300 = (2ⁿ - 1) - 4,43 gerade n = 12.

- Supernova
Die Experimente mit den übereinander befindlichen und abprallenden Bällen lassen sich aber auch zur ernsthaften Deutung einiger interessanter physikalischer Erscheinungen heranziehen. Nach einer astrophysikalischen Vorstellung läuft eine Supernova so ab, dass ein Stern sich zunächst schneller und schneller kontrahiert. Der innere Kern verdichtet sich immer mehr. Schließlich läuft eine Schockwelle vom inneren, festen Kern des Sterns nach außen und trifft dort auf die sich noch zum Kern hin bewegenden äußeren, leichten Teile der Schale des Sterns. Beim Aufeinandertreffen können Teile der äußeren Schale bis auf relativistische Geschwindigkeiten beschleunigt werden und wegfliegen. Der Stern explodiert förmlich. Dieser Ablauf ähnelt sehr dem zu Beginn betrachteten Fall von zwei Bällen: Der schwere Ball fliegt schon nach oben (außen) und gibt dem noch auf ihn zufliegenden, kleinen Ball einen großen Impuls, der den kleinen Ball dann auf eine hohe Geschwindigkeit bringt. Aus diesem Beispiel heraus ist auch der in Amerika gebräuchliche Name 'Astrojax' zu deuten.

- Raumsonden / Swingby-Manöver
Die amerikanischen Pioneer- und Voyager-Sonden werden mit dem sogenannten Swingby-Manöver (auch sling shot) auf hohe Geschwindigkeiten gebracht. Dabei geht es um die raffinierte Ausnutzung sich anziehender Kräfte. Die Sonde fliegt dem sich nähernden Planeten (z.B. Jupiter) entgegen. Sie fliegt aber nicht direkt auf ihn zu, sondern in einer - hyperbolischen - Bahn um ihn herum. Da sie danach fast in eine entgegengesetzte Richtung fliegt, nimmt sie die Bahngeschwindigkeit des Planeten Jupiter mit sich und erhöht so ihre eigene Geschwindigkeit enorm. Erst dadurch ist eine energiesparende Erkundung erdferner Planeten möglich.

3. Literatur

U. Eberth, J. Eberth, P. von Brentano: Neues zur Drei-Ball-Pyramide, Physik und Didaktik 22 (1994), 251-254

Stark Verlag