
 |
Mechanik |
Inbetriebnahme
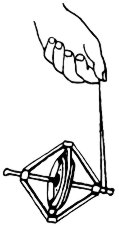
| Stecken Sie die beiliegende Schnur durch die Öffnung an der Achse des Gyroskops (Abb. 1)und wickeln Sie die Schur mit gut anliegenden Windungen spiralig auf die Achse. Nehmen Sie die Halterung des Kreisels fest in die Hand und ziehen Sie gleichmäßig kräftig an der Schnur. Das Gyroskop erreicht Drehzahlen von etwa 5000 Umdrehungen pro Minute. Insgesamt kann es bis fast 10 Minuten lang rotieren.
Bitte passen Sie bei allen Experimenten auf, dass Ihnen das Gyroskop nicht herunterfällt, da sich sonst die Achse verbiegen kann und dann durch die entstehende Unsymmetrie das Gyroskop unrund läuft. Sorgen Sie für eine weitere Unterlage, auf die das Gyroskop eventuell fallen kann. |
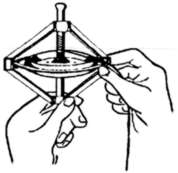 Abb. 1 |
| Balancierakt (Balancing Act)
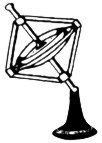
Plazieren Sie das rotierende Gyroskop mit einem Achsenende auf den beiliegenden Ständer. Es dreht sich - je nach Winkel zwischen Drehachse und Ständerachse und je nach Drehzahl - schneller oder langsamer und fällt nicht herunter. Erst wenn die Rotation des Gyroskops nachgelassen hat, hält es sich nicht mehr auf dem Ständer. Diese Drehung auf dem Ständer nennt man Präzession. |
 |
Drehung mit einer Schnur (Loop the loop) Setzen Sie das rotierende Gyroskop mit einem Achsenende in eine Schlaufe der Antriebsschnur. Wie bei dem vorherigen Experiment dreht sich das Gyroskop um die Schur ohne Herunterzufallen. |
 |
|
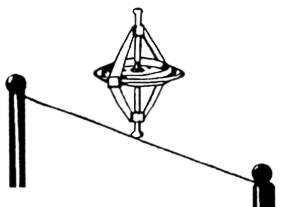 |
Balance auf einer Schnur (On the Edge)
Setzen Sie das rotierende Gyroskop mit dem geschlitzten Ende der Achse auf die gespannte Antriebsschnur. Es fällt nicht herunter. |
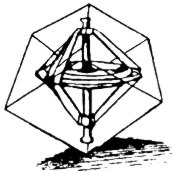
Magischer Würfel (Magic Box)
Setzen Sie das rotierende Gyroskop in den durchsichtigen Verpackungswürfel oder noch besser in einen gleichgroßen, undurchsichtigen Papier- bzw. Pappwürfel und stellen Sie den Würfel mit dem rotierenden Gyroskop bleibt auf der Ecke stehen. |
 |
Etwas Physik
Gyroskope bzw. Kreisel sind nicht nur ein altes und weitverbreitetes Spielzeug. Technisch ausgefeilte Kreisel sind z. B. in Kreiselkompassen enthalten und ermöglichen eine wetterunabhängige Navigation. Dabei macht man sich zunutze, dass schnell rotierende Kreisel ihre Drehachse immer stabil, d.h. raumfest zu halten versuchen. Wirkt auf einen Kreisel eine Kraft sinkrecht zu Rotationsachse, versucht der Kreisel wiederum dazu senkrecht auszuweichen. Das ist der Grund dafür, dass der rotierende Kreisel nicht vom Ständer oder von der Schnur herunterfällt, sonder eine sogenannte Präzession ausführt.
Einige grob quantitative Abschätzungen lassen sich zum Gyroskop durchführen:
Mit einem Stroboskop kann man die Drehzahl dieses Gyroskops bestimmen. Es ergeben sich etwa 5000 Umdrehungen pro Minute, d. h. 83,3 Umdrehungen/Sekunde. Daraus folgt eine Kreisfrequenz von ω = 524 s-1. Die mit bloßem Auge messbare Präzessionsfrequenz fP des rotierenden Gyroskops auf dem Ständer beträgt etwa 1 Umdrehung in 3 Sekunden, d. h.
ωp = 2 · π · fp = 2,1 s-1.
Das Gesamtgewicht des Gyroskops mit Halterung beträgt
G = 0,106 kg · 9,81 ms-2 = 1 N;
das Gyroskop alleine hat eine Masse von 86 g. Der Abstand des Schwerpunkts des rotierenden Gyroskops vom Auflagepunkt beträgt a = 4,8 cm. Damit kann man das Trägheitsmoment IG des Gyroskops ausrechnen:
IG = a · G/(ωP · ω) = 0,048 m · 1 N/(2,1 s-1 · 524 s-1) = 4,4 · 10-5 kgm2.
Man kann das Trägheitsmoment des Kreisels auch direkt abschätzen. Stellt man sich die gesamte Masse des Gyroskops vom 86 g auf einem Ring mit einem Radius von etwa
r ≈ 2,5 cm konzentriert, ergibt sich
IG = m · r2 ≈ 0,086 kg · 0,0252 m2 = 5,4 · 10-5 kgm2.
Bei den hier verwendeten, groben Abschätzungen ist die Übereinstimmung mit dem vorigen Wert ziemlich befriedigend.
Literatur
Otto Ernst Berge: Spielzeug im Physikunterricht (A.1 unserer Bibliothek im Labor für Physik
und Didaktik, Raum G 0.40)
Stark Verlag