
 |
Schwingungen und Wellen |
SW 1.10 klopfender SpechtDie genaue Analyse der Bewegungsabläufe eines scheinbar einfachen Spielzeugspechts führt auf verhältnismäßig komplexe Differentialgleichungen. Die theoretische Mechanik befasst sich aktuell mit Fragestellungen des hier auftretenden Reibstoßes, der eine große Bedeutung für die Technik hat. |
 |
1. Übersicht
Tippt man den oben an der Stange befindlichen Specht an, wippt er mit dem Schnabel an die Stange klopfend nach unten.
Erfunden wurde der Spielzeug-, Klopf- oder Pickspecht möglicherweise um die Jahrhundertwende im Erzgebirge, seit jeher ein Zentrum für ingeniöse Holzspielwaren. Andere unsichere - Aussagen deuten auf einen Ursprung im Fernen Osten hin. (Wir wären sehr interessiert an Hinweisen auf die Entstehung.) Es gibt den Specht in Riesenausführungen mit einer Stangenlänge von über einem Meter und ebenso in einer Miniaturführung, die in einem "Uberraschungsei" Platz hat. Auch andere Realisierungen z. B. mit einem Schmetterling sind uns bekannt.
| Genauer besehen, besteht das Spielzeug aus einer Muffe, die über eine Stange geschoben wird, und einem Vogel, der mit einer Feder an dieser Muffe befestigt ist (Abb. 1). Schiebt man die Muffe ans obere Ende der Stange und lässt sie vorsichtig los, so bleibt der Specht dort in Ruhe stehen. Der Grund dafür, dass er nicht abrupt die Stange hinunterrutscht, ist in der speziellen Konstruktion der Muffe zu suchen. Sie hat gegenüber der Stange etwas Spiel, so dass sie sich unter dem Gewicht des Spechts schräg stellt und verkantet. Dieser Mechanismus wird Selbsthemmung genannt und funktioniert um so zuverlässiger, je schwerer der Specht ist oder genauer gesagt, je größer die aus dem Spechtgewicht resultierende, durch die Feder übertragene, senkrecht zur Stange stehende Kraftkomponente am Muffenpunkt B ist (Abb. 1). Eine Verstärkung dieser Kraftkomponente, der Normalkraft, führt zu einer gleichzeitigen Verstärkung derjenigen tangentialen Kontaktkraft, die überwunden werden muss, um einen Übergang vom Haften zum Gleiten zu ermöglichen. Haften ist also für den ruhenden Specht eine sichere Angelegenheit, die nur dann durch Gleiten ersetzt würde, wenn der Specht zu leicht wäre. |
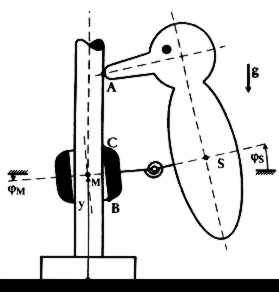 Abb. 1: Schematische Darstellung des Spechts |
Dieser Selbsthemmungsmechanismus tritt nicht nur beim Specht auf, sondern wird in vielen technischen Systemen ausgenützt. Einfache Beispiele sind Keile, die etwa das Zuschlagen von Türen verhindern sollen, oder spezielle halbkreisförmige Steigeisen, die zum Erklettern von Holzmasten von Stromleitungen benutzt werden. In abgeschwächter Form findet man den Verstärkungsmechanismus der Reibkraft auch bei den auflaufenden Bremsbacken der im Fahrzeugbau verwendeten Trommelbremsen.
2. Theorie
Der Vorgang des abwechselnden Pickens und Rutschens, der sich immer wieder mit verblüffender Regelmäßigkeit einstellt, wird hauptsächlich durch die Muffe bestimmt. Je nachdem, ob sie die Stange berührt oder nicht, schaltet sie den oben beschriebenen Selbsthemmungsmechanismus ein oder aus und regelt damit die Schwingungen des Spechts.
Dass sich die Schwingung nach einer bestimmten Zeit immer in der gleichen Art und Weise einstellt, unabhängig davon, wie der Specht losgelassen wird, ist in einem internen Regelmechanismus begründet, der das System immer in den in Abbildung 2 gezeigten Schwingungszustand zurückführt, bei dem ein energetisches Gleichgewicht zwischen zugeführter und dissipierter Energie vorliegt.
Der Specht rutscht pro Schwingungsperiode um eine bestimmten Betrag die Stange herunter. Damit nimmt die Lageenergie des Systems ab und wird die Muffe dem Specht zugeführt und in Schwingungsenergie umgewandelt. Mit dieser zugeführten Energie können die bei den Stößen und Gleitphasen auftretenden Verluste ausgeglichen werden. So dissipiert bei dem hier berechneten Specht ca. 50% der zugeführten Energie beim Schnabelstoß und 38% beim unteren Muffenstoß. Die restlichen 12% teilen sich in die beiden oberen Muffenstöße und die Gleitphasen auf.
Der Rückkoppelungsmechanismus, der den Specht immer in diesen Gleichgewichtszustand zwingt, ist relativ einfach zu verstehen, wenn man bedenkt, dass die Energiezufuhr fast ausschließlich in den Freiflugphasen erfolgt. Wird der Specht zum Beispiel so angestoßen, dass die Amplitude der Schwingung zu groß ist, so führ dies dazu, dass er die Freiflugphasen schneller passiert. Damit bleibt ihm weniger Zeit, um nach unten zu fallen; der pro Periode nach unten zurück gelegte Weg nimmt also ab. Dies bedeutet aber, dass dem Specht weniger Lageenergie zugeführt wird und in Schwingungsenergie umgesetzt werden kann. Bei zu kleinen Amplituden drehen sich die Verhältnisse gerade um. Insgesamt ergibt sich also das folgende Verhalten: sind die Amplituden der Schwingung zu groß, so wird die Energiezufuhr vermindert. Sind die Amplituden zu klein, so wird sie erhöht. Damit wird zwangsläufig ein Zustand erreicht, bei dem die Amplituden gerade so groß sind, dass sie zur zugeführten Energie passen und nicht mehr verändert werden.
Die Schwingung, die zu diesem Zustand gehört, heißt Grenzzykel ((3) - Abb. 2). Dieser ist sehr stark anhängig von den eingesetzten Parametern (Reibungskoeffizient, Innendurchmesser und Länge der Muffe, Ausgangsbedingungen). Es kann sogar chaotisches Verhalten auftreten oder der Specht fällt im Extremfall einfach die Stange hinunter, ohne zu picken.
Solche selbsterregten Systeme, die nach einem internen Regelmechanismus arbeiten, trifft man in der Technik sehr häufig an. Hierzu gehören zum Beispiel das Knarren von Türangeln, das Quietschen von Kreide auf der Tafel, das Tragflügelflattern bei Flugzeugen oder das Hochgeschwindigkeitspendeln bei Motorrädern. Die diesen Schwingungen zugrunde liegenden Rückkopplungsmechanismen sind zum Teil äußerst komplex und können nur mit großem Aufwand analysiert werden.
3. Das Schwingungsverhalten
Eine detaillierte Analyse des Schwingungsverhaltens gewinnt man zum Beispiel aus einer numerischen Auswertung der Bewegungsgleichungen des in Abbildung 1 dargestellten Systems. Die drei Koordinaten y, φM und φs beschreiben die vertikale Lage des Muffenschwerpunktes Y, den Neigungswinkel der Muffe, und den des Spechts.
Weiter müssen drei mögliche Kontaktpunkte A, B, C vorgesehen werden (Abb. 1), denn der Schnabel kann an die Stange schlagen, und die Muffe kann an ihrem unteren oder oberen Ende die Stange berühren.
Abbildung 2 zeigt die Phasenkurve der Spechtschwingung , also die Winkelgeschwindigkeit φ des Spechts in Abhängigkeit des aktuellen Neigungswinkels φs.
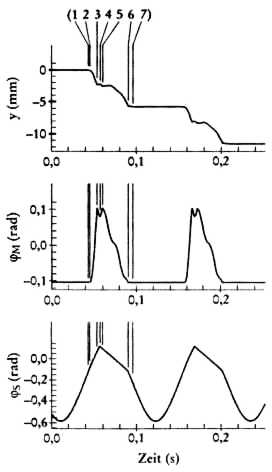
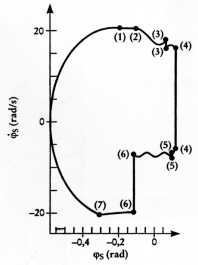 Abb. 2 - oben: Die Phasenkurve stellt die Winkelgeschwindigkeit fs des Spechts in Abhängigkeit des aktuellen Neigungswinkels φ dar. Die eingeklammerten Nummern beziehen sich auf die in Tabelle 1 wiedergegebenen Zustandsübergänge. Abb.3 - rechts: Aus dem zeitlichen Verlauf der vertikalen Lage y des ;Muffenwinkels φM und des Neigungswinkels φs lassen sich die abrupten Übergänge deutlich ersehen. |
 |
Wir starten die Diskussion bei Punkt (7). Hier hat die Muffe am Punkt B Kontakt mit der Stange und haftet. Der Specht schwingt nach unten durch, bis er seine tiefste Stellung bei einem Winkel von knapp -0,6 rad erreicht. Dort kehrt sich seine Bewegung um, er ist jetzt auf dem Weg nach oben. Je weiter er nach oben schwingt, desto mehr entspannt sich die Feder zwischen Specht und Muffe. Dies bedeutet aber, dass auch die am Kontaktpunkt B wirkende Normalkraft zurückgeht und schließlich am Punkt (1) der Selbsthemmungsmechanismus aufgelöst wird. Die Muffe beginnt nach unten zu gleiten, währen der Specht wegen seiner Trägheit weiter nach oben schwingt. Die Normalkraft nimmt deswegen weiter ab, bis sich bei (2) die Muffe von der Stange löst. Zwischen (2) und (3) hat kein Teil der Muffe mehr Kontakt mit der Stange; das System befindet sich jetzt in der sogenannten Freiflugphase, in der keine der drei Koordinaten mehr blockiert ist.
Freiflugphasen zeichnen sich dadurch aus, dass sie Systemen die maximal mögliche Bewegungsfreiheit geben, was sich hier in einer Überlagerung von drei Schwingungszuständen äußert: Specht und Muffe rotieren wie ein einziger starrer Körper, Specht und Muffe schwingen gegeneinander und lenken dabei die Feder aus. Obwohl sich der Specht nach oben bewegt, wird in dieser Phase die Muffe wegen der gemeinsamen Rotation nach unten gedrückt, wie im Zeitverlauf y (t) in der Abbildung 3 zu sehen ist. Am Punkt (3) trifft nun das obere Muffenende C auf die Stange. Dieser Stoß ist allerdings für das System von untergeordnetem Interesse, denn der entsprechende Kontakt löst sich auch sofort wieder auf. Kurze Zeit später erreicht der Schnabel des sich immer noch nach oben bewegenden Spechts die Stange. Der erfolgende Reibstoß (4) führt zu einer sprunghaften Umkehr der Spechtgeschwindigkeit, wie man an der senkrechten Linie in der Phasenkurve sehen kann. Nach einem zweiten kleinen oberen Muffenstoß (5) ist das System wieder in der Freiflugphase, wobei sich jetzt der Specht nach unten bewegt. Hier wird der zweite Teil der Muffenfallhöhe pro Schwingungsperiode erzielt. Zusätzlich ist in der Phasenkurve sehr deutlich eine Schlangenlinie zu erkennen, die der hochfrequenten Schwingung der Muffe gegenüber dem Specht entspricht. In Punkt (6) hat sich das Gesamtsystem so weit gedreht, dass das untere Muffenende B die Stange berührt. Es erfolgt ein ausgeprägter Reibstoß, der die Fallgeschwindigkeit der Muffe drastisch reduziert, allerdings hier nicht ganz ausreicht, um Haften zu bewirken. Deswegen schließt sich eine kurze Gleitphase an. An Punkt (7) kommt die Muffe auf grund von Reibung zum Stillstand. Dies bedeutet, dass der Selbsthemmungsmechanismus aktiv werden kann, und der Specht nach unten schwingt.
Damit ist die in Abbildung 2 gezeigte Schwingung einmal durchlaufen, und der Prozess beginnt von vorne. Die Bewegung des Spechts zeichnet sich vor allem dadurch aus, dass laufend Koordinaten durch Stöße und Reibung gesperrt oder freigegeben werden. Solche Systeme, die abschnittsweise durch unterschiedlich viele Differentialgleichungen beschrieben werden müssen, haben in der Praxis eine große Bedeutung. Die mathematischen Methoden dazu sind auch erst in den letzten Jahren entwickelt worden. Reib- und Stoßprobleme treten, erwünscht oder unerwünscht, in nahezu allen technischen Systemen auf. Man denke nur an Schlagbohrmaschinen. an das sogenannte Kupplungsrupfen in Kraftfahrzeugen, oder an Stöße, die beim Auflaufen von Ketten auf ihre Kettenräder entstehen.
Tabelle 1: Zustandsübergänge der Bewegung. Hierin bedeuten: H: Haften, G: Gleiten und S: Seperation.
| Punkte in Abb. 2. |
Kontakt | Bewegung |
| (1) | B | H→G |
| (2) | B | G→S |
| (3) | C | S→S |
| (4) | A | S→S |
| (5) | C | S→S |
| (6) | B | S→G |
| (7) | B | G→H |
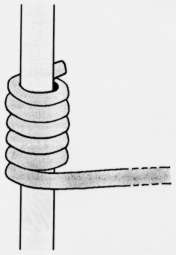 Abb.4: selbstgedrehte Spiralfeder als Halterung |
4. grundsätzlicher Aufbau Der grundsätzliche Aufbau des Spielzeugspechts kann relativ leicht realisiert werden. Eine- metallene- Blattfeder aus einem Aktenhefter wird mit einem Loch auf eine Metall- oder Holzstange mit einem Durchmesser von 5 mm geschoben. Am anderen Ende wird durch Probieren ein geeignetes Gewicht befestigt. Dieses System schwingt schon pendelnd hinunter. Eine zweite Möglichkeit besteht darin, einen dünnen Draht (z. B. gerade gebogene Büroklammer) als Spiralfeder eng um einen 3 bis 5 mm dicken Metallstab zu drehen. Wenige Windungen genügen bereits (Abbildung 4). Am Ende der selbstgewickelten Feder wird ein leichter Gegenstand, z. B. ein Schmetterling aus buntbemalter Pappe, befestigt. Es zeigt sich hier übrigens, dass der Schnabelstoß des zu Beginn erwähnten Spechts für die Funktion gar nicht notwendig ist. Bei diesen einfachen Eigenkonstruktionen lassen sich allerlei Parameter variieren. Durch Änderung der Drahtlängen, -duchmesser, Endgewichte, Material der Stange ergeben sich verschiedene Frequenzen. |
Literatur
(1) F. Pfeiffer, Mechanische Systeme mit unstetigen Übergängen, Ingenieur- Archiv 54, 232 (1984).
(2) Ch. Glockner, F. Pfeiffe, Multiple Impacts with Friction in Rigid Multibody System, in: Non linear Dymanics (Hrsg. A. H. Nayfeh), Kluwer Academic Publishers, ersch. 1995.
(3) H.-J. Schlichting, Der Pickspecht- ein sich selbst organisierendes System, Naturwissenschaften im Unterricht, Physik, 36, 37 (1988).
(4) J. Wittmann, Trickkiste 1, Experimente, wie sie nicht im Physikbuch stehen, bsv München 1983.
(5) C. Wirth, Demonstration der Selbststeuerung einer Blattfederschwingung, Praxis der Naturwissenschaften, Physik, 26,19 (1977)
Die Autoren
Christoph Glockner, geb. 1962, Studium des Maschinenwesens in München. Seit 1989 als wissenschaftlicher Assistent am Lehrstuhl B für Mechanik der TU- München. Betätigungsfeld: Dynamik von Starrkörpersystemen mit einseitigen Bindungen und Trockenreibung.
Christian Ucke, Physikdepartment E 20, Technische Universität München