
 |
O2 Wellenoptik |
Verwandte Begriffe
Interferenz, Wellenlänge, Brechungsindex, Lichtgeschwindigkeit, Phase, virtuelle Lichtquelle.
1. Prinzip
Licht wird durch 2 Spiegel in der Michelson-Anordnung zur Interferenz gebracht. Durch Verschieben des einen Spiegels mit der Mikrometerschraube wird die Wellenlänge bestimmt.
|
2. Aufgabe Bestimmung der Wellenlänge des Lichts des verwendeten Lasers. 3. Aufbau und Durchführung Der Versuchsaufbau erfolgt gemäß Abb. 1. Um möglichst viele Interferenzfiguren zu erhalten, werden erst beide Spiegel des Interferometers justiert; hierbei wird zunächst die Linse entfernt. Der Laser- strahl trifft den halbdurchlässigen Spiegel unter 45°, wobei der Strahl geteilt wird. Die beiden Teilstrahlen werden an den Spiegeln reflektiert und treffen auf den Schirm auf. Mit den beiden Justierschrauben an einem der Spiegel werden beide Lichtpunkte zur Deckung gebracht. |
 Abb. 1: Experimenteller Aufbau zur Messung von Wellenlängen mit dem Michelson Interferometer |
Bringt man die Linse in den Strahlengang, so werden die Lichtpunkte aufgewertet, und auf dem Schirm beobachtet man Interferenzmuster (Streifen, Kreise). Durch sorgfältiges Nachjustieren kann man ein Interferenzbild von konzentrischen Kreisen erhalten.
Zur Wellenlängenmessung dreht man das Schraubenmikrometer in eine beliebige Anfangsposition, für die das Zentrum der Kreise dunkel ist. Das Schraubenmikrometer wird nun im gleichen Drehsinn (wegen Spindelspiel) weitergedreht und dabei die hell-dunkel-Perioden gezählt. Der Weg des Spiegels ist am Schraubenmikrometer abzulesen und durch zehn zu teilen (Hebeluntersetzung 1:10). Sollte der Mittelpunkt der Kreise aus dem Leuchtfleck laufen, so muss nachjustiert werden.
4. Theorie und Auswertung
Fallen auf einen Ort 2 Wellen derselben Frequenz ω verschiedener Amplitude und verschiedener Phase, so überlagern sie sich zu
y = a1 sin (ωt - α1) + a2 sin (ωt - α2)
Die resultierende Welle kann geschrieben werden als
y = A sin (ωt - α)
mit der Amplitude
A2 = a12 + a22 + 2a1a2 cosδ (Formel 1)
und
δ = α1 - α2
In einem Michelson Interferometer wird Licht an einer halb durchlässigen Glasplatte in 2 Teilbündel aufgespalten (Amplitudenteilung), an 2 Spiegeln reflektiert und hinter der Glasplatt wieder zur Interferenz gebracht.
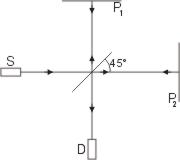 Abb.2: Michelson Anordnung zur Interferenz |
Zwischen Lichtstrahl und Glasplatte wird eine Linse gebracht, so dass die Lichtquelle im Brennpunkt liegt, da nur ausgedehnte Lichtflecke Interferenzringe zeigen können.
Ersetzt man den wirklichen Spiegel M2 durch sein virtuelles Bild M2', das durch Reflexion an der Glasplatte gebildet wird, so erscheint ein Punkt P der wirklichen Lichtquelle als die Punkte P' und P'' der virtuellen Lichtquellen L1 und L2. |
| Aufgrund der verschiedenen Lichtwege ist mit den Bezeichnungen der Abb. 3 die Phasendifferenz:
δ = (2π/λ) 2d cosΘ λ ist die Wellenlänge des verwendeten Lichts. Die Intensitätsverteilung ist nach (Formel 1) für al = a2 = a I ~ A2 = 4a2 cos2(δ/2) Maxima treten also auf, wenn δ Vielfaches von 2π ist, also mit (2) 2d cosΘ = mλ•m = 1, 2,..... (Formel 4) d. h. es gibt Kreisringe für ein fest gewähltes m und d, da Θ konstant bleibt (siehe Abb. 3). |
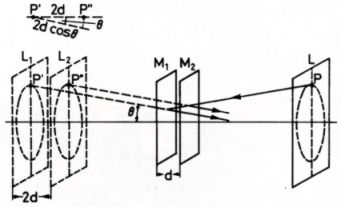 Abb. 3: Bildung von Kreisringen bei Interferenz |
Verändert man die Lage der des beweglichen Spiegels Ml, so dass d z. B. abnimmt, so wird nach (4) auch der Ringdurchmesser abnehmen, da m ja für diesen Ring fest ist. Es verschwindet also jedesmal ein Ring, wenn d um λ/2 verkleinert wird. Für d = 0 verschwindet das Ring-Muster.
Sind M1, und M2 nicht parallel, erhält man gekrümmte Streifen, die für d = 0 in gerade Streifen übergehen.
Um die Wellenlänge des Lichtes zu messen, wurden 500 Ringwechsel gezählt. Dabei wurde eine Verschiebung des Spiegels um 158 µm gemessen. Daraus ergibt sich die Wellenlänge
λ = 632 nm.